Orbitals, Fermions and Gradients: Getting started with Tequila¶
pip install git+https://github.com/aspuru-guzik-group/tequila.git
Slides in notebook form: github.com/kottmanj/talks_and_material
In [2]:
import tequila as tq
import numpy
Warmup:¶
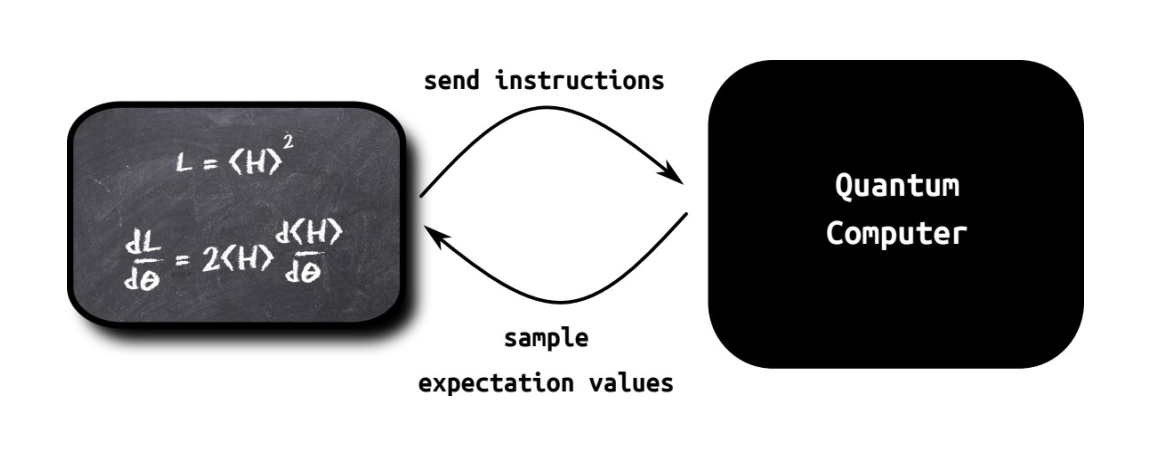
Original idea for quantum computers: Simulate nature
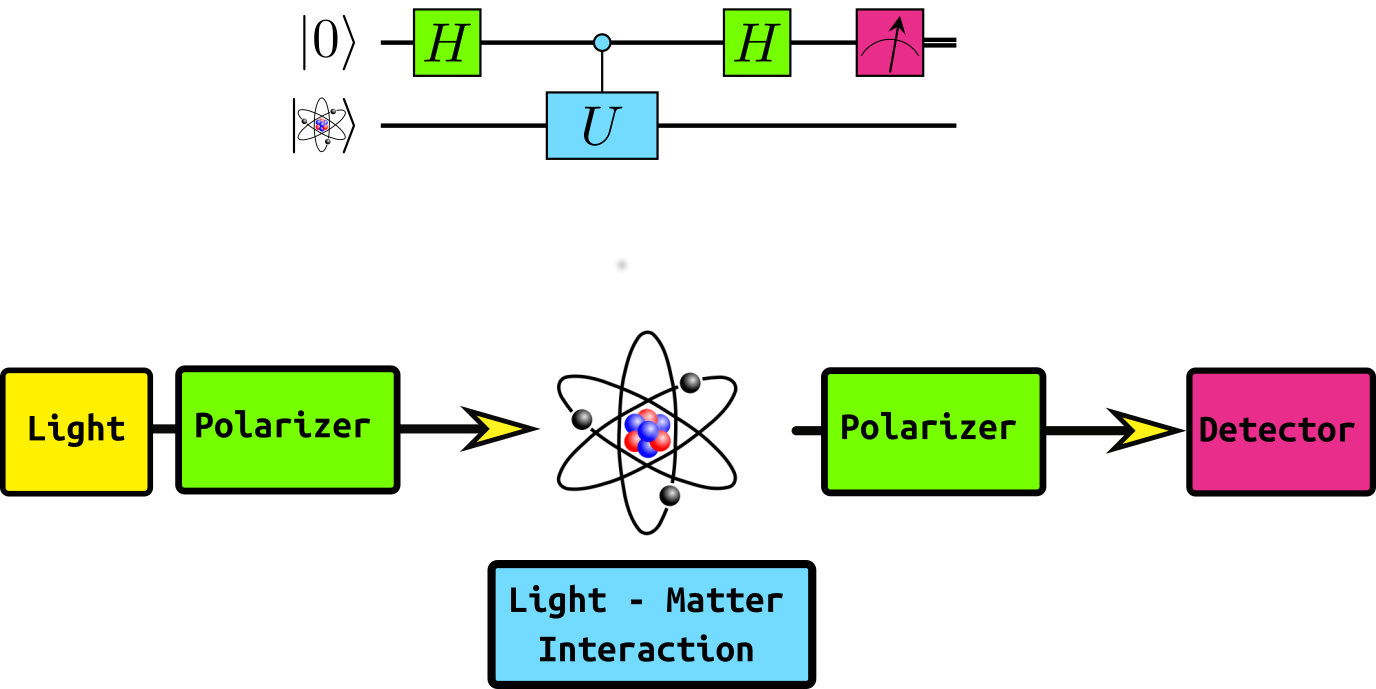
Assume: $U = e^{i\frac{\theta}{2}G}$ with hermitian matrix $G$ and $\theta=2\pi$.
For simplicity: Assume eigenvalues of $G$ are $0$ and $1$
Concrete example: $$ G = \sigma_x + 1 $$
In [3]:
G = 0.5*(tq.paulis.X(1)+1.0)
In [4]:
val, vec = numpy.linalg.eigh(G.to_matrix())
eigenstates = []
for i in range(2):
wfn = tq.QubitWaveFunction.from_array(vec[:,i])
print("energy = {:+2.5f}, wfn=".format(val[i]), wfn)
eigenstates.append(wfn)
In [5]:
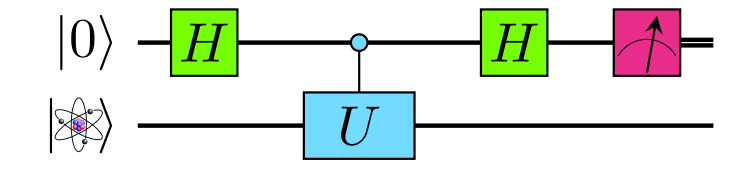
a=2*numpy.pi
cU = tq.gates.Trotterized(generator=G, angle=a, control=0)
U = tq.gates.H(0) + cU + tq.gates.H(0)
wfn = tq.simulate(U)
print("wavefunction after circuit:\n", wfn)
In [53]:
Qp = tq.paulis.Qp(0) # Qp = |0><0| = 0.5(Z+1)
wfn2 = Qp(wfn)
wfn2 = wfn2.normalize()
print("wavefunction after measurements:\n",wfn2)
fidelity = numpy.abs(wfn2.inner(eigenstates[0]))**2
print("fidelity with eigenstate 0:", fidelity )
A Toy VQE¶
Example before: Quantum Phase Estimation (measure eigenvalues of Hermitian operator)
Now: Variational Quantum Eigensolver (minimize expectation value of Hermitian operator)
$$ \min_{\theta} \langle H \rangle_{U(\theta)} $$In [7]:
H = 0.5*(tq.paulis.X(0) + 1.0)
U = tq.gates.Ry(target=0, angle="a")
E = tq.ExpectationValue(H=H, U=U)
In [8]:
result = tq.minimize(E)
Simulate and Compile Objectives¶
In [9]:
# simulate objectives
energy1 = tq.simulate(E, variables={"a": -numpy.pi/2})
# compile objectives and use as functions
f = tq.compile(E)
energy2 = f({"a":-numpy.pi/2})
# use different backends and options
energy3 = tq.simulate(E, variables={"a": -numpy.pi/2}, backend="cirq", samples=1000)
Beyond Groundstates¶
Overlap punishment:
$$ S^2\left(\phi, \psi\right)= \lvert\langle \phi \vert \psi \rangle\rvert^2 = \langle Q_+ \rangle_{U_\phi^\dagger U_{\psi}} , \quad Q_+ = \lvert 00\dots0 \rangle\langle 00\dots0 \lvert$$In [10]:
Uex = tq.gates.Ry(angle="b", target=0)
S2 = tq.ExpectationValue(H=tq.paulis.Qp(0), U=Uex+U.dagger())
opt_gs = {"a":-0.5*numpy.pi}
L = tq.ExpectationValue(H=H, U=Uex) + 10.0*S2
In [11]:
result_ex = tq.minimize(L,
initial_values=opt_gs,
variables=["b"])
In [12]:
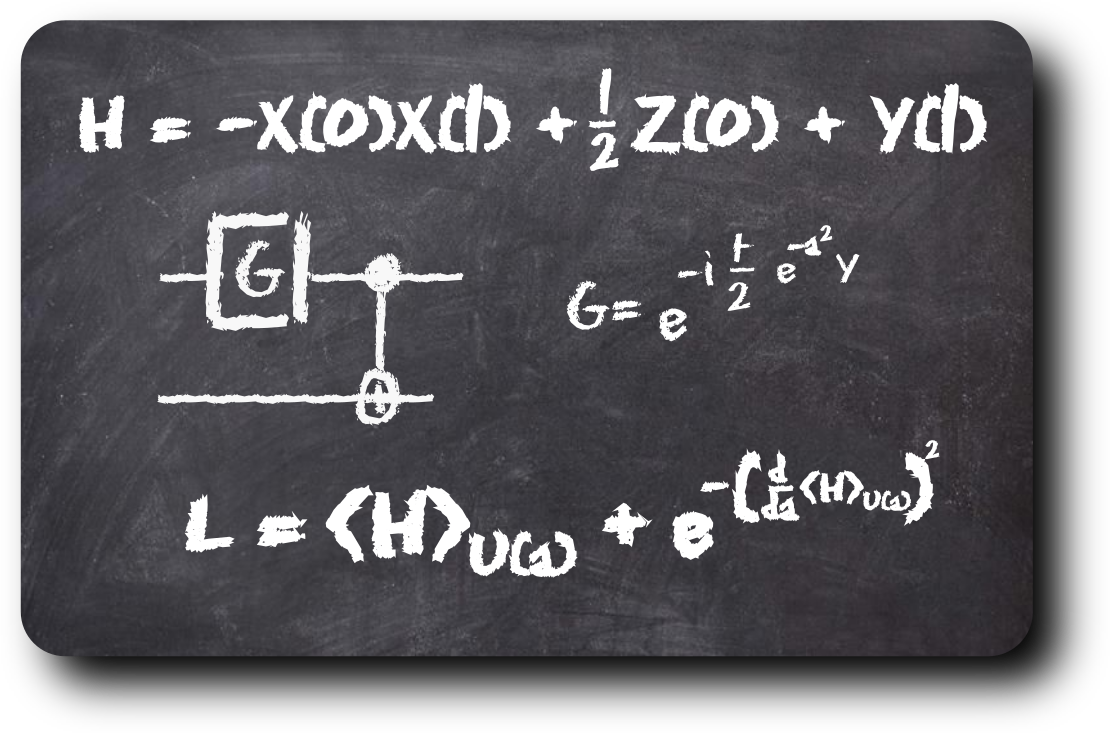
a = tq.Variable("a")
angle = (-a**2).apply(tq.numpy.exp)
U = tq.gates.Ry(angle=angle*numpy.pi, target=0)
U += tq.gates.X(target=1, control=0)
H = tq.QubitHamiltonian("-1.0X(0)X(1)+0.5Z(0)+Y(1)")
E = tq.ExpectationValue(H=H, U=U)
dE = tq.grad(E, "a")
objective = E + (-(dE**2)).apply(tq.numpy.exp)
f = tq.compile(objective)
In [13]:
import matplotlib.pyplot as plt
start=-2.0
stop=2.0
values = {}
for value in [start + i/100*(stop-start) for i in range(100)]:
values[value] = f({"a":value})
plt.plot(list(values.keys()), list(values.values()))
plt.show()
In [14]:
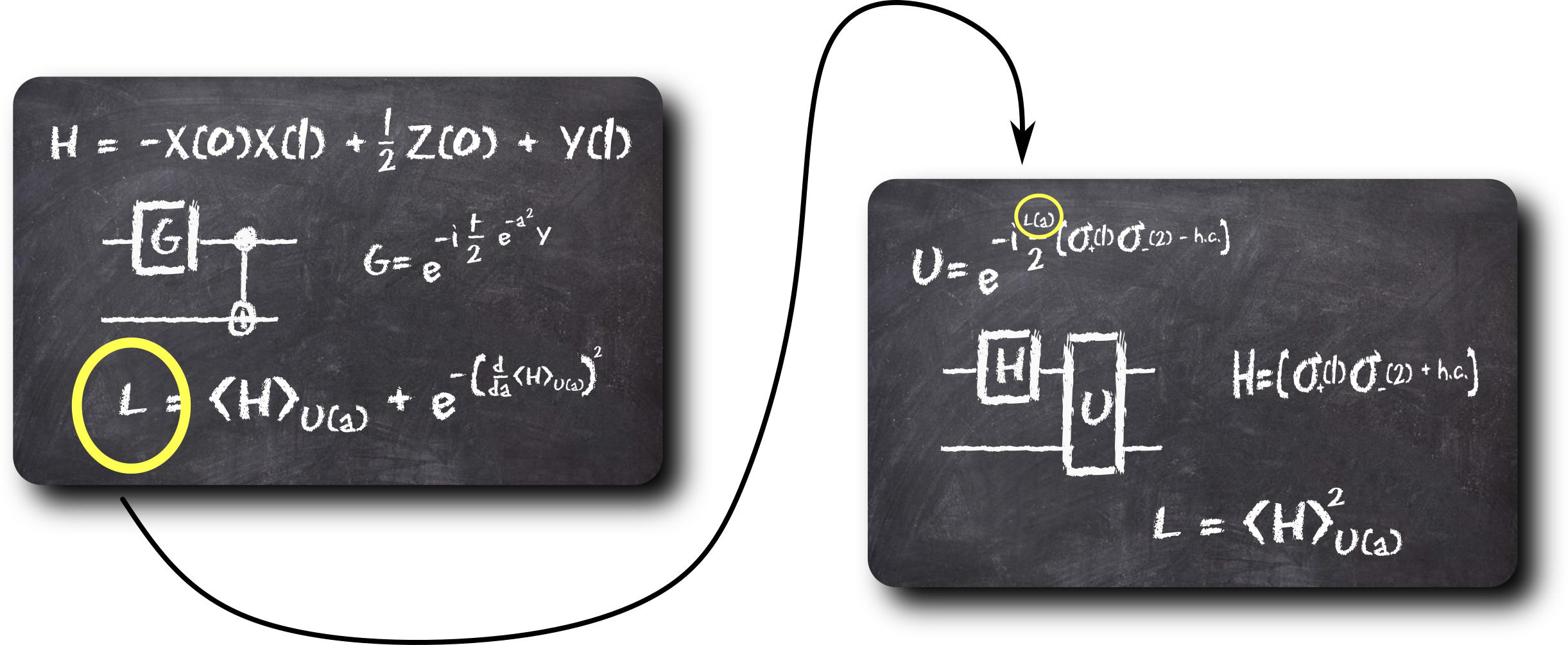
H = tq.paulis.Sp(0)*tq.paulis.Sm(1)
H += tq.paulis.Sm(0)*tq.paulis.Sp(1)
U = tq.gates.X(0)
U += tq.gates.QubitExcitation(angle=f, target=[0,1])
L2 = tq.ExpectationValue(H=H, U=U)**2
f2 = tq.compile(L2)
In [15]:
import matplotlib.pyplot as plt
start=-2.0
stop=2.0
steps=100
values = {}
for value in [start + i/steps*(stop-start) for i in range(steps)]:
values[value] = f2({"a":value})
plt.plot(list(values.keys()), list(values.values()))
plt.show()
Example: Meta-VQE¶
A. Cervera-Lierta, JSK, A. Aspuru-Guzik, ArXiv:2009.13545
Learn the relation of a parameters in the Hamiltonian and in the circuit
In [16]:
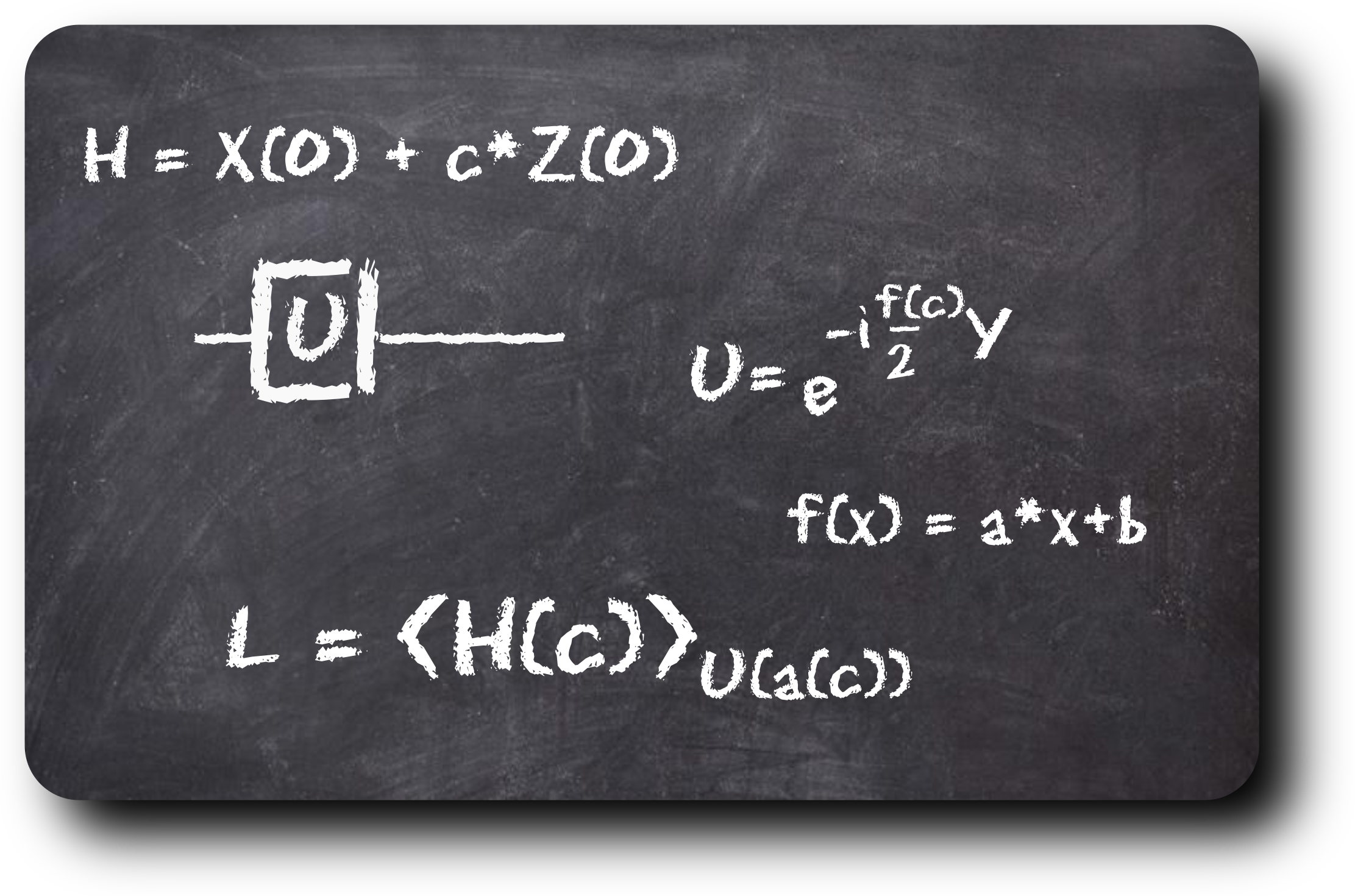
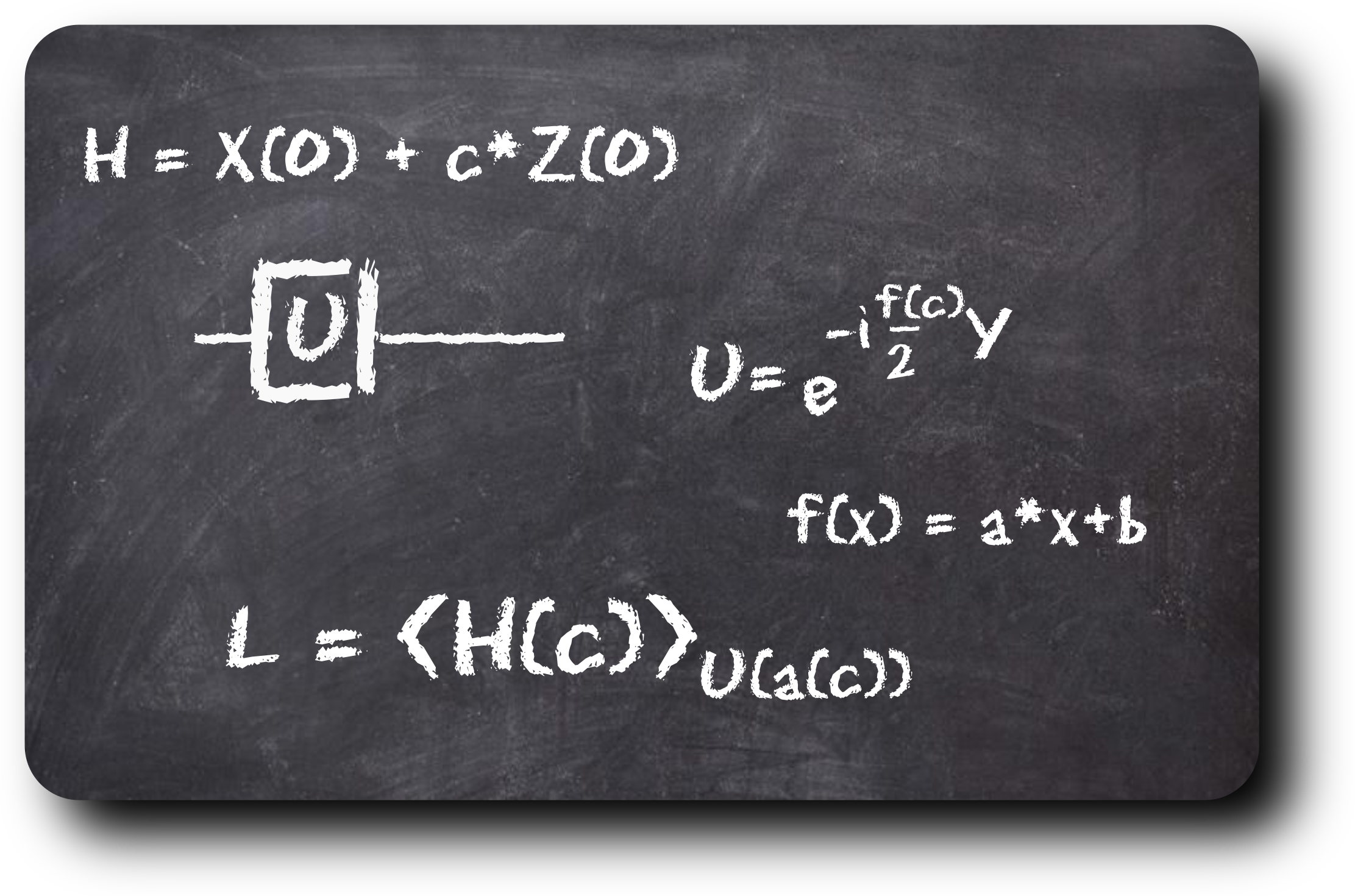
def meta_angle(x):
a = tq.assign_variable("a")
b = tq.assign_variable("b")
return x*a-b
def make_H(x):
return tq.paulis.X(0) + x*tq.paulis.Z(0)
def make_U(angle):
angle = tq.assign_variable(angle)
return tq.gates.Ry(target=0, angle=angle*numpy.pi)
Training¶
In [17]:
training_points = [0.0, 0.5, 1.0]
meta_objective = 0.0
for x in training_points:
meta_objective += tq.ExpectationValue(H=make_H(x), U=make_U(meta_angle(x)))
meta_objective = 1.0/len(training_points)*meta_objective
In [18]:
meta_vqe_result = tq.minimize(meta_objective)
Testing¶
In [19]:
test_points=[0.0 + x/100 for x in range(100)]
predicted_angles = {}
opt_angles = {}
for x in test_points:
predicted = meta_angle(x)(variables=meta_vqe_result.variables)
predicted_angles[x] = predicted
objective = tq.ExpectationValue(H=make_H(x), U=make_U("x"))
opt = tq.minimize(objective, silent=True, initial_values=predicted)
opt_angles[x] = opt.variables["x"]
In [20]:
plt.plot(list(predicted_angles.keys()), list(predicted_angles.values()), label="predicted", marker="o", markersize=5)
plt.plot(list(opt_angles.keys()), list(opt_angles.values()), label="opt", marker="x", markersize=3)
plt.legend()
plt.show()
In [21]:
def meta_angle(x):
a = tq.assign_variable("a")
b = tq.assign_variable("b")
c = tq.assign_variable("c")
d = tq.assign_variable("d")
return b*x**2 + c*x + d
In [23]:
plt.figure()
plt.plot(list(predicted_angles.keys()), list(predicted_angles.values()), label="predicted", marker="o", markersize=5)
plt.plot(list(opt_angles.keys()), list(opt_angles.values()), label="opt", marker="x", markersize=3)
plt.legend()
plt.show()
Example: Quantum Chemistry¶
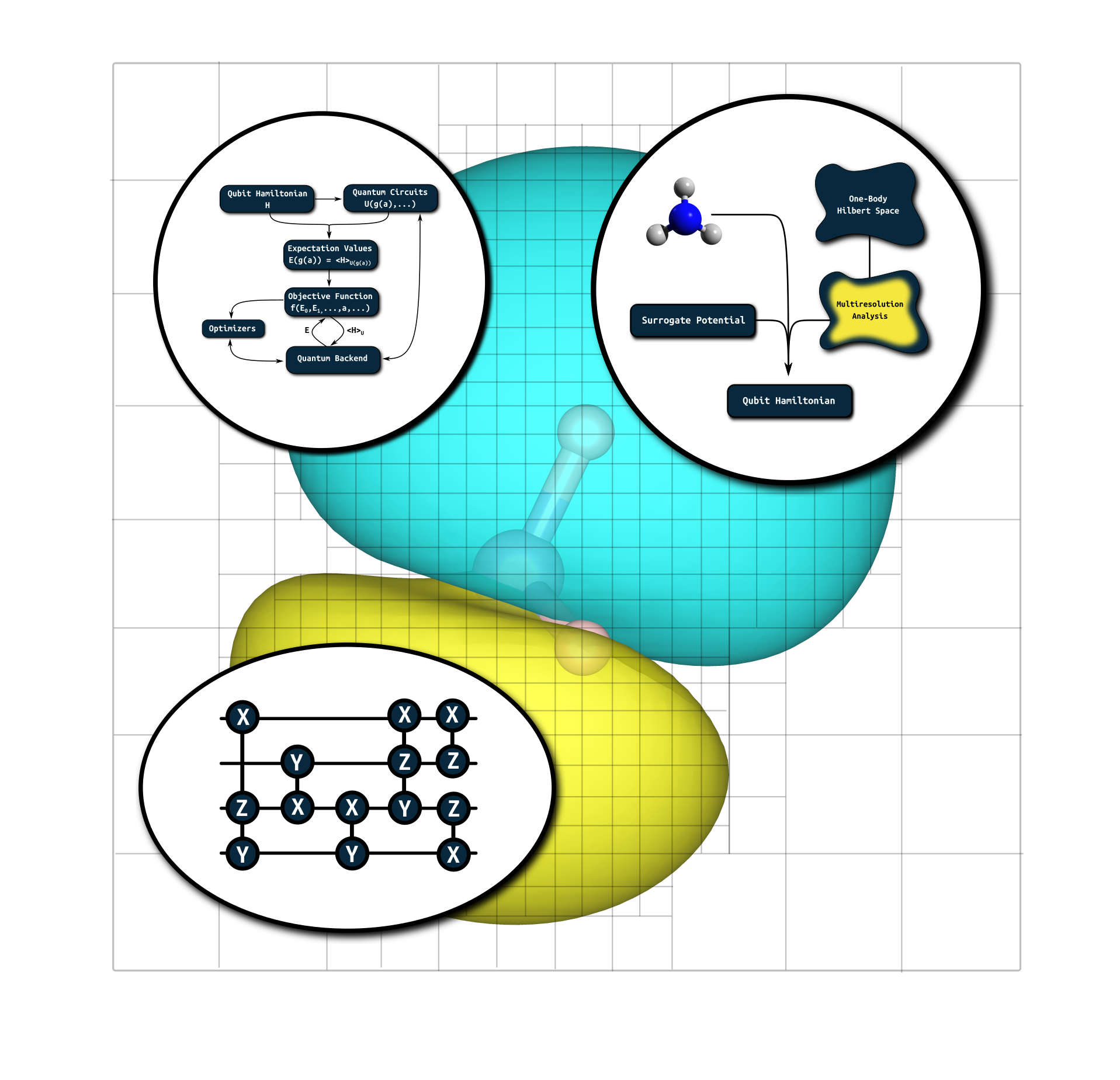
Dependencies¶
- Basis set representation: Psi4
conda install psi4 -c psi4 - Basis-set-free: Madness
follow instructions on this fork: github.com/kottmanj/madness - Tutorials: github.com/aspuru-guzik-group/tequila-tutorials
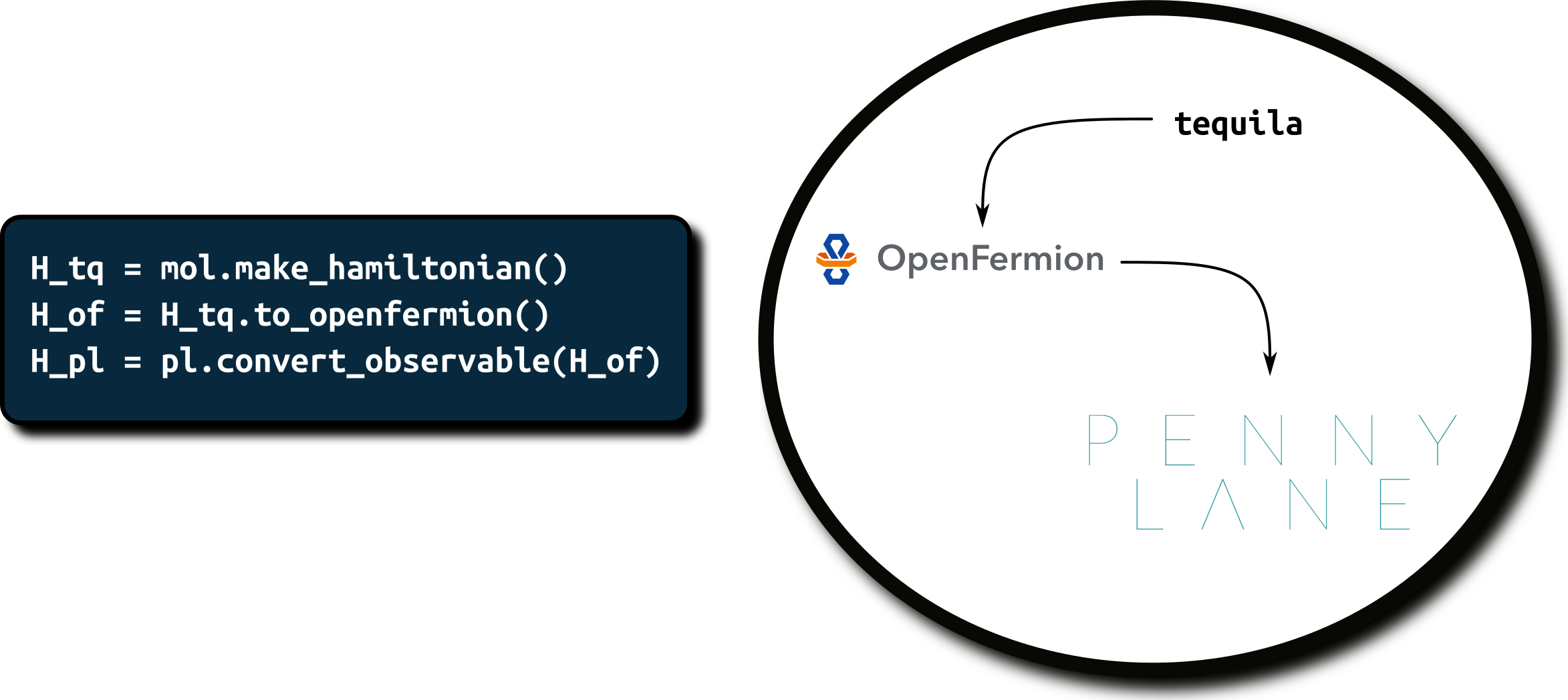
Molecular Hamiltonian in Qubit Representation¶
In [25]:
geomstring = "H 0.0 0.0 0.0\nH 0.0 0.0 {R}".format(R=0.7)
mol = tq.Molecule(geometry=geomstring,basis_set="sto-3g")
H = mol.make_hamiltonian()
In [26]:
print(H)
Hartree-Fock Reference State¶
In [27]:
U = mol.prepare_reference()
E = tq.ExpectationValue(H=H, U=U)
hf_energy = tq.simulate(E)
print("EHF = {:+2.5f}".format(hf_energy))
In [28]:
print(E)
In [29]:
E = tq.ExpectationValue(H=H, U=U, optimize_measurements=True)
print(tq.compile(E, backend="qiskit"))
In [54]:
geomstring = "H 0.0 0.0 0.0\nLi 0.0 0.0 {R}".format(R=0.7)
mol = tq.Molecule(geometry=geomstring, basis_set="sto-3g",
transformation="BravyiKitaev")
print(mol)
Active Spaces¶
In [31]:
geomstring = "H 0.0 0.0 0.0\nLi 0.0 0.0 {R}".format(R=0.7)
active={"A1":[1,2]}
mol = tq.Molecule(geometry=geomstring,
basis_set="sto-3g",
active_orbitals=active)
H = mol.make_hamiltonian()
Manually Construct an Ansatz¶
In [32]:
U = tq.gates.Ry(angle="a", target=0)
U += tq.gates.X(1)
U += tq.gates.X(target=1, control=0)
U += tq.gates.X(target=2, control=1)
U += tq.gates.X(target=3, control=2)
U += tq.gates.X(target=1)
In [33]:
tq.draw(U)
Optimize the Ansatz¶
In [34]:
E = tq.ExpectationValue(H=H, U=U)
result = tq.minimize(E)
energy_np = numpy.linalg.eigvalsh(H.to_matrix())[0]
energy_fci = mol.compute_energy("fci")
In [35]:
print("VQE = {:2.5f}".format(result.energy))
print("FCI = {:2.5f}".format(energy_fci))
print("Numpy = {:2.5f}".format(energy_np))
Manually construct an UCC ansatz¶
In [36]:
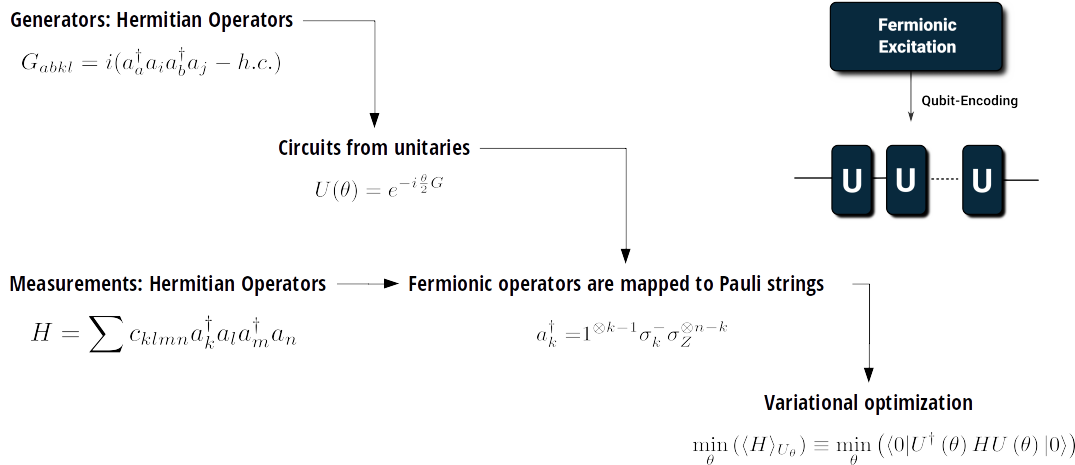
G0213 = mol.make_excitation_generator(indices=[(0,2),(1,3)])
Uex = tq.gates.Trotterized(generator=G0213, angle="a")
U = mol.prepare_reference() + Uex
In [37]:
tq.draw(U)
In [38]:
E = tq.ExpectationValue(H=H, U=U)
result = tq.minimize(E)
Gradient Aware Construction¶
In [39]:
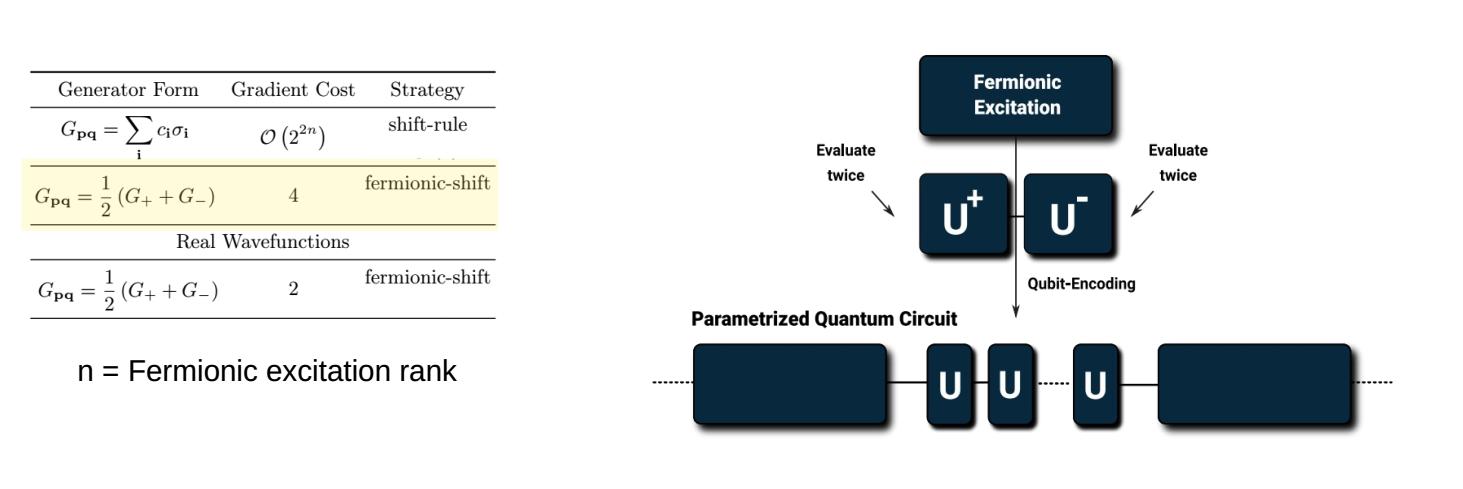
Uex = mol.make_excitation_gate([(0,2),(1,3)], "a")
U = mol.prepare_reference() + Uex
E = tq.ExpectationValue(H=H, U=U)
In [40]:
result = tq.minimize(E)
Quantum Chemistry: Constructing the Hamiltonian¶
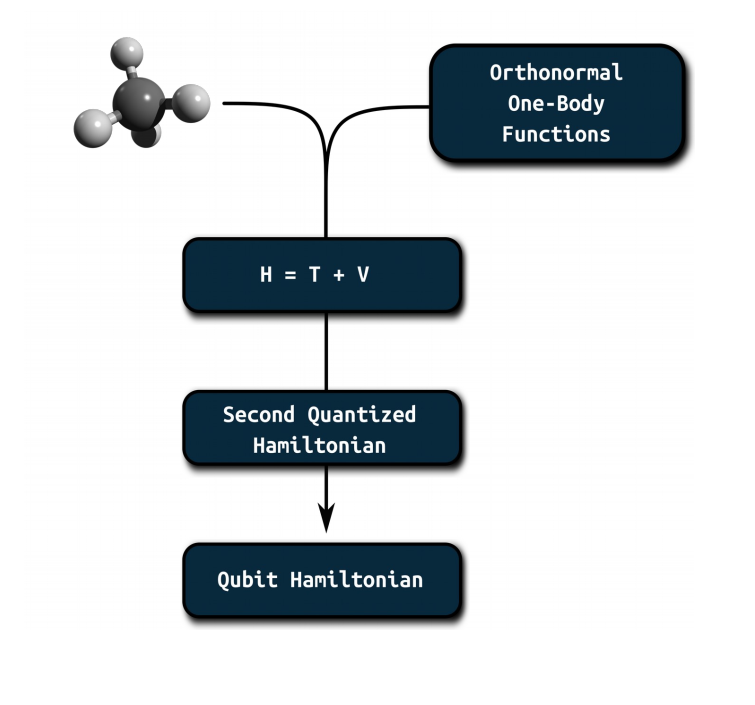
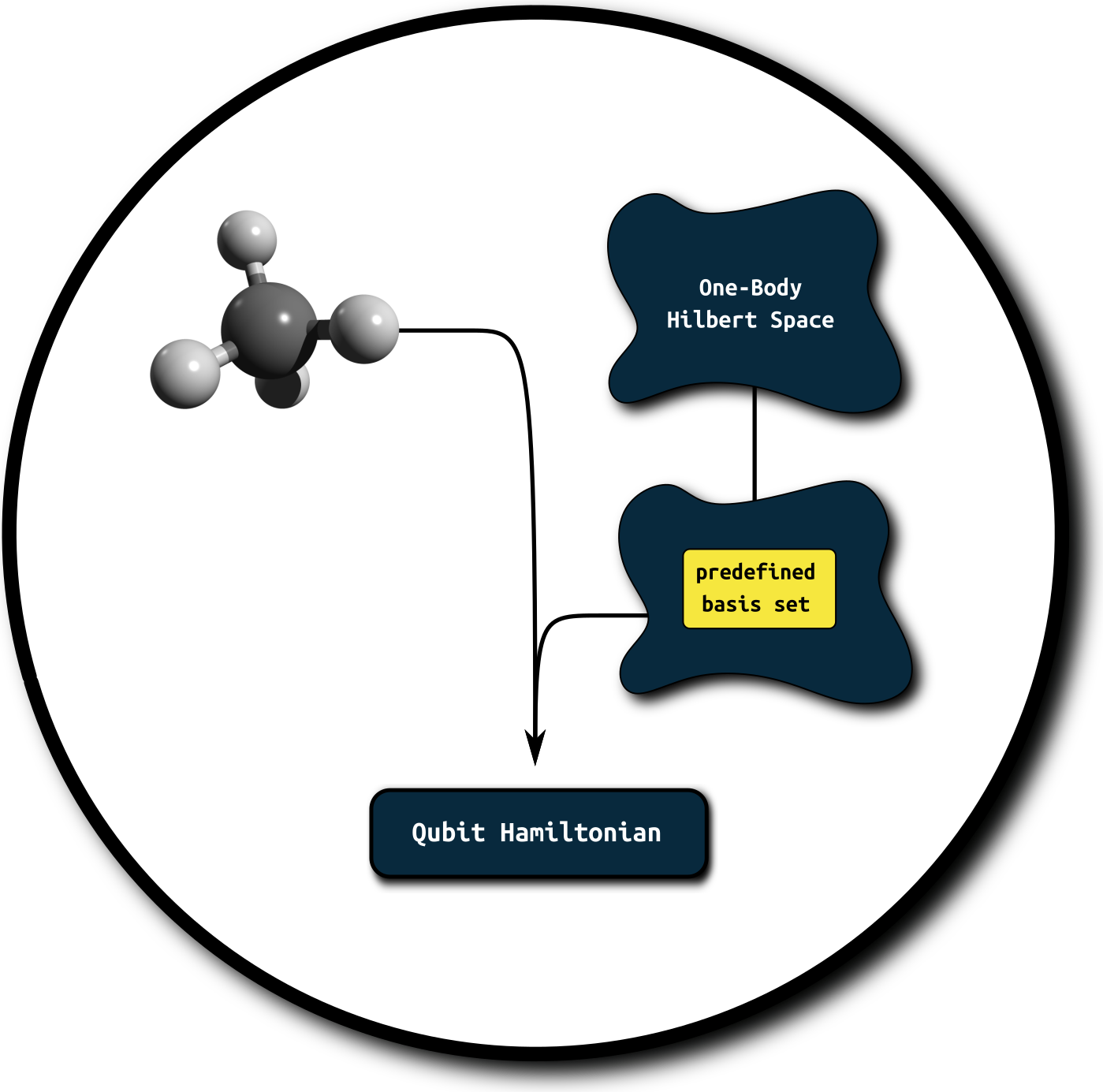
- Well developed classical machinery
- Unknown numerical error
- Accurate results require large basis sets
- High level of expertise required from the user
In [42]:
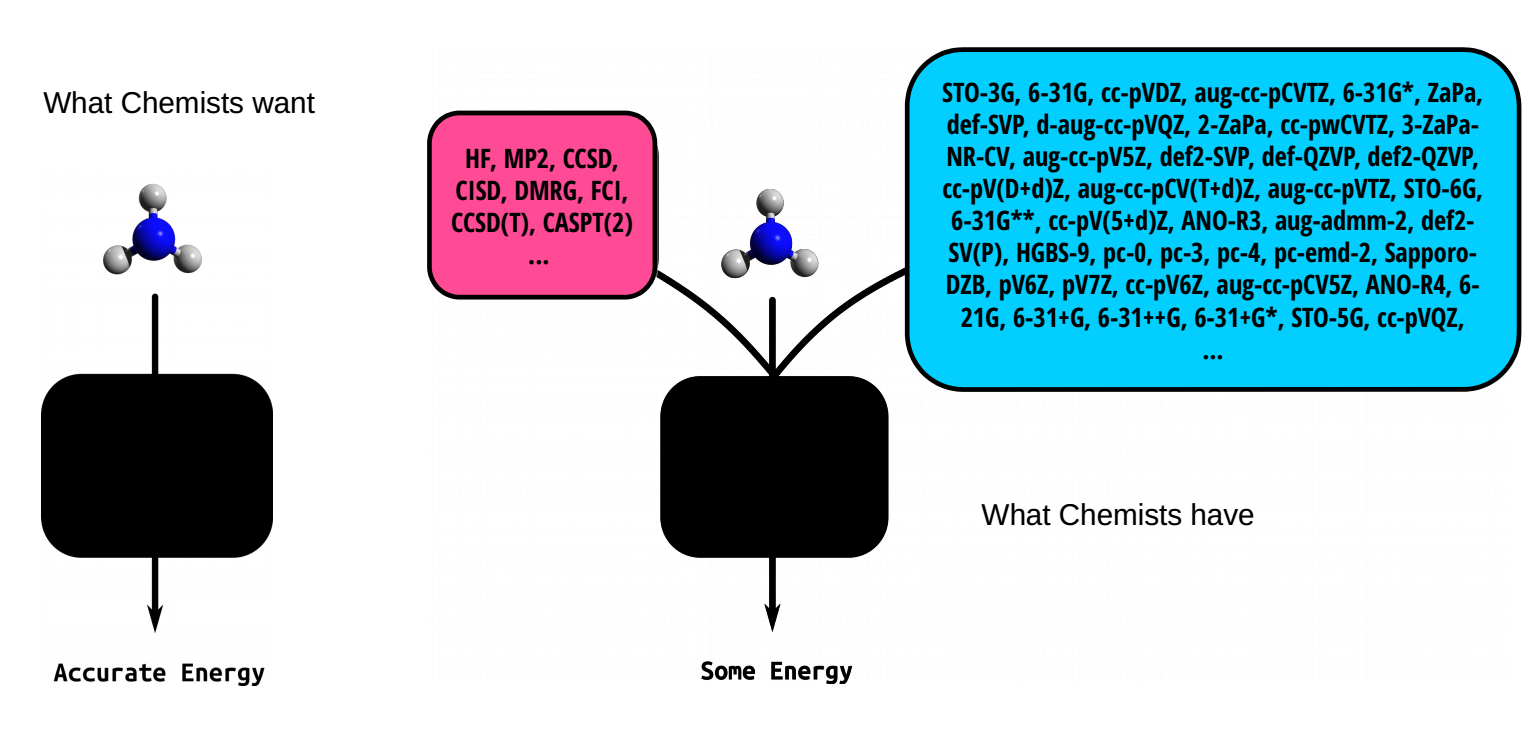
mol = tq.Molecule(geometry=geomstring, basis_set="cc-pVDZ")
print(mol.make_hamiltonian().n_qubits)
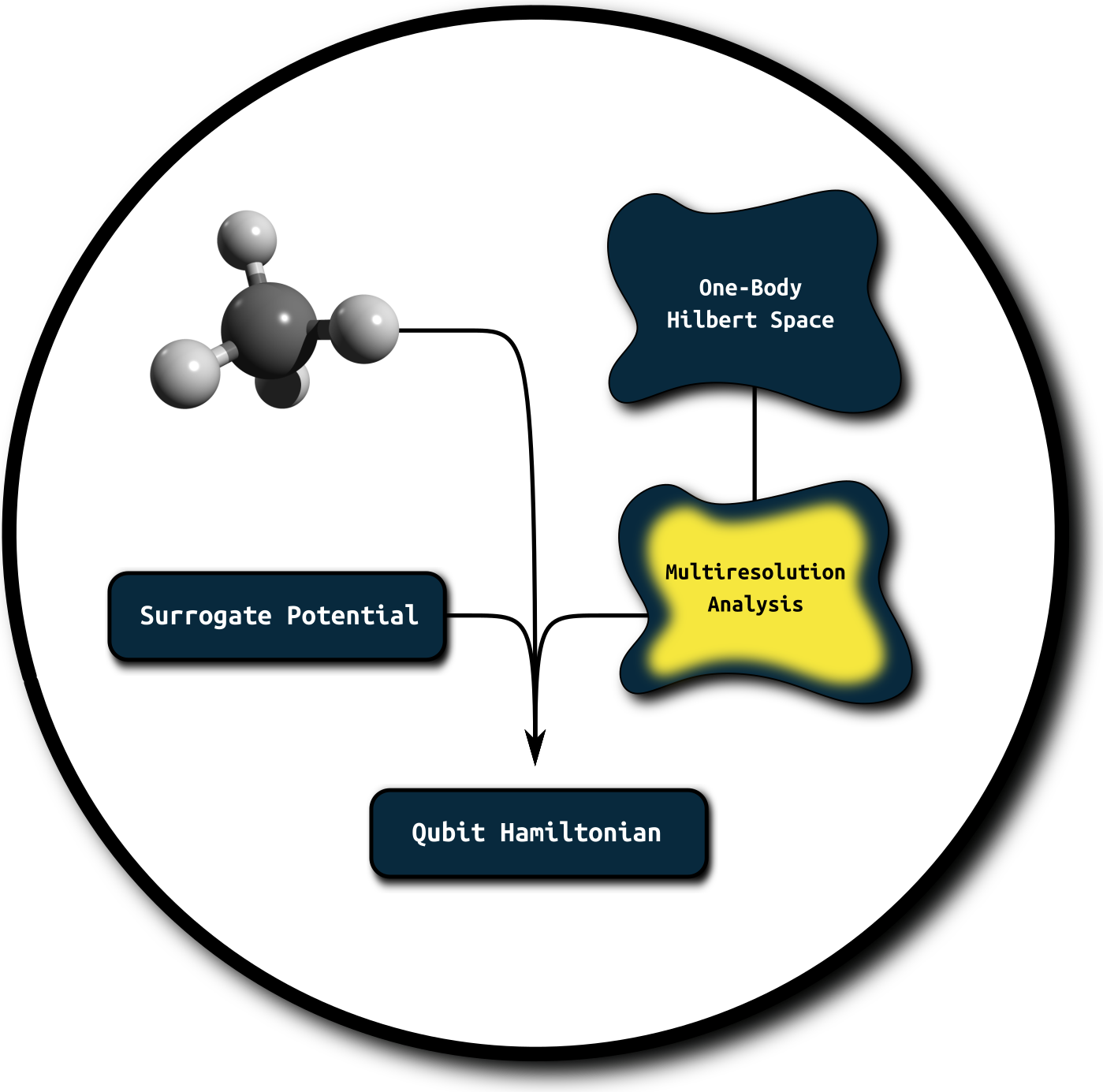
- Basis-set-free
- Physically interpretable limitations
- Compact (save qubits)
- Natural order on orbitals
- Low level of expertise required from user
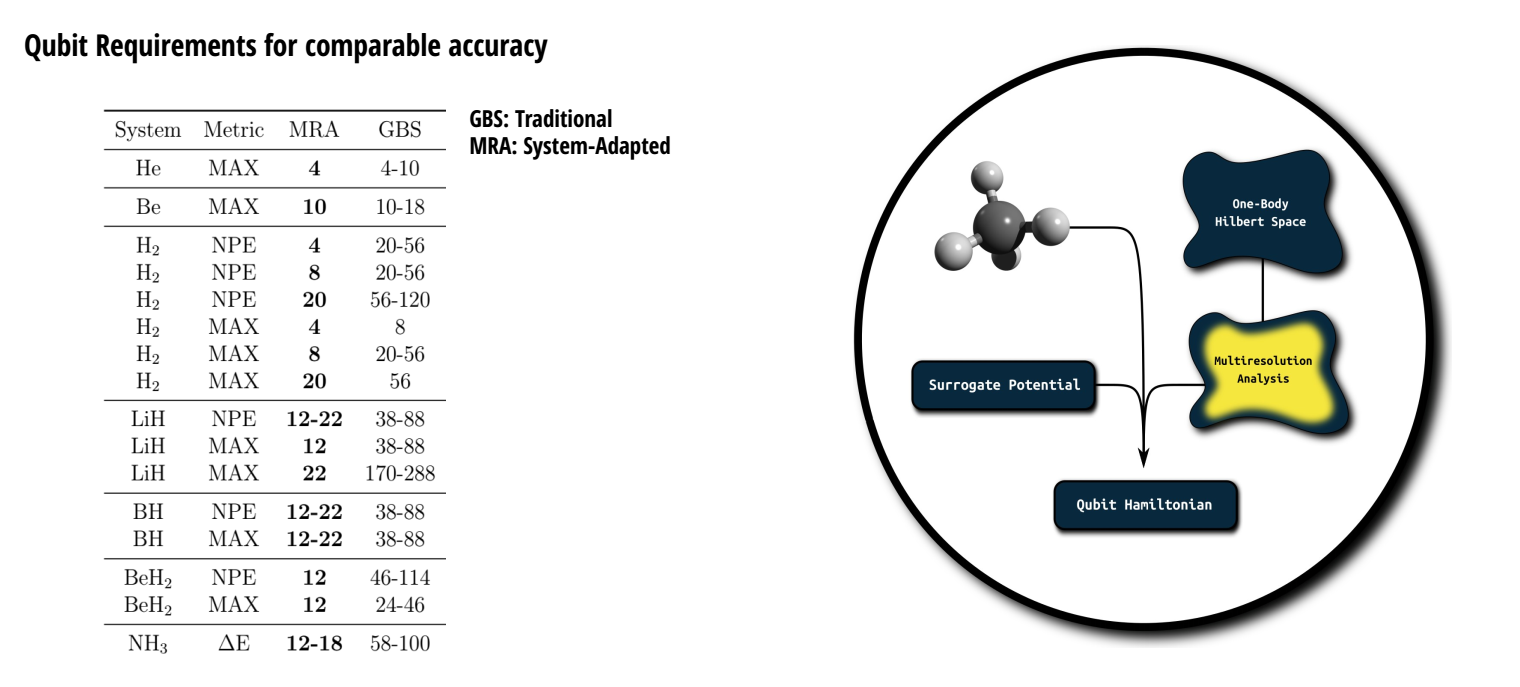
More¶
Basis-set-Free VQE:
JSK, P. Schleich, T. Tamayo-Mendoza, A. Aspuru-Guzik doi.org/10.1021/acs.jpclett.0c03410
Surrogate Model (PNO-MP2):
JSK, F. A. Bischoff, E. F. Valeev doi.org/10.1063/1.5141880
Tequila backend: Madness
R.J. Harrison et.al. doi.org/10.1137/15M1026171
MRA basics:
doi.org/10.18452/19357 (Chapter 2)
Review on classical applications:
F.A. Bischoff, doi.org/10.1016/bs.aiq.2019.04.003
In [7]:
mol = tq.Molecule(geometry="Li 0.0 0.0 0.0\nH 0.0 0.0 1.6",
n_pno=4,
executable=madness_exe,
name="lih_1.6")
H = mol.make_hamiltonian()
U = mol.make_pno_upccgsd_ansatz(include_singles=False)
E = tq.ExpectationValue(H=H, U=U)
In [8]:
print(mol)
In [75]:
result = tq.minimize(E)
Example: Adaptive Solvers¶
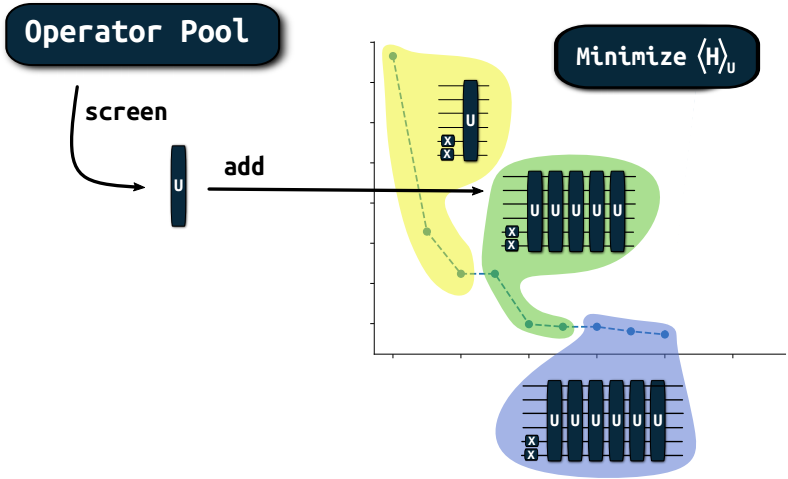
Original approaches:
Ryabynkin, Yen, Genin, Izmaylov, doi.org/10.1021/acs.jctc.8b00932
Grimsley, Economou, Barnes, Mayhall doi.org/10.1038/s41467-019-10988-2
Example: Adaptive Solvers¶
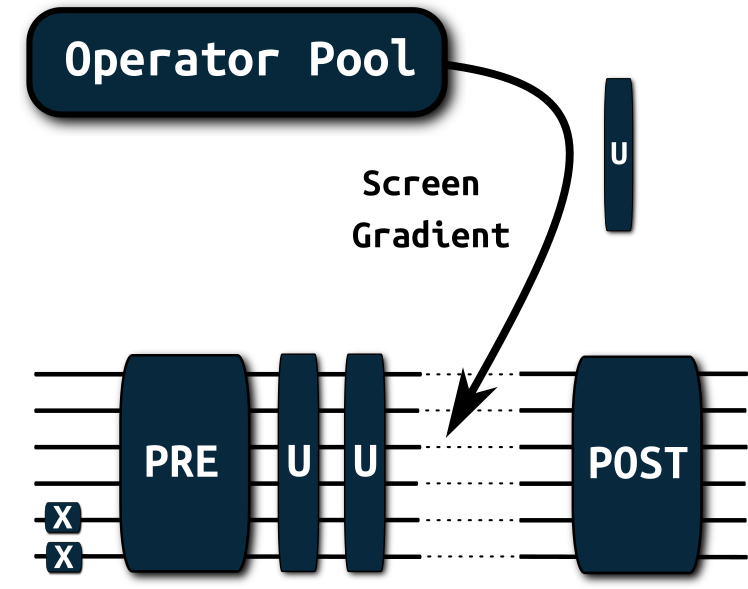
Tequila implementation:
JSK, Anand, Aspuru-Guzik. doi.org/10.1039/D0SC06627C
More examples on github
In [9]:
operator_pool = tq.apps.adapt.MolecularPool(molecule=mol,
indices="UpCCGSD")
solver = tq.apps.adapt.Adapt(operator_pool=operator_pool,
H=mol.make_hamiltonian(),
Upre=mol.prepare_reference())
result = solver()
Example: Molecular Meta-VQE¶
In [47]:
def meta_angle(R):
a = tq.assign_variable("a")
b = tq.assign_variable("b")
c = tq.assign_variable("c")
d = tq.assign_variable("d")
return a*(-(b*R-c)**2).apply(tq.numpy.exp) + d
def make_U(mol, angle):
U = mol.prepare_reference()
U += mol.make_excitation_gate([(0,2),(1,3)], angle)
return U
In [48]:
geomstring = "H 0.0 0.0 0.0\nH 0.0 0.0 {R}"
training_points = [0.5, 1.0, 1.5, 3.0]
meta_objective = 0.0
for R in training_points:
mol = tq.Molecule(name="H2_R_{R:1.4f}".format(R=R), geometry=geomstring.format(R=R), n_pno=1, executable=madness_exe)
H = mol.make_hamiltonian()
U = make_U(mol, meta_angle(R))
E = tq.ExpectationValue(H=H, U=U)
meta_objective += E
meta_objective = 1.0/len(training_points)*meta_objective
meta_vqe_result = tq.minimize(meta_objective, initial_values={"b":1.0, "c":1.0})
In [50]:
from matplotlib import pyplot as plt
plt.figure()
plt.plot(list(predicted_angles.keys()), list(predicted_angles.values()), label="predicted", marker="o", markersize=5)
plt.plot(list(opt_angles.keys()), list(opt_angles.values()), label="opt", marker="x", markersize=3)
plt.title("angle")
plt.legend()
Out[50]:
In [51]:
from matplotlib import pyplot as plt
plt.figure()
plt.plot(list(predicted_energies.keys()), list(predicted_energies.values()), label="predicted", marker="o", markersize=5)
plt.plot(list(opt_energies.keys()), list(opt_energies.values()), label="opt", marker="x", markersize=3)
plt.title("energy")
plt.legend()
Out[51]:
Suggestions¶
- Overview: Arxiv:2011.03057
- Code & Tutorials: github.com/aspuru-guzik-group/tequila
- Install:
pip install git+https://github.com/aspuru-guzik-group/tequila.git - Not to be confused with the Minecraft server manager :-)
pip install tequila
In [ ]: