Tequila in a Nutshell

  • Tequila is software development kit for quantum algorithms focused on abstraction
  • It allows to define abstract functions from combinations of quantum expectation values
  • Frontend and "blackboard-style" API are inspired by madness
  • Backend-agnostic implementation is inspired by pennylane
  • Tequila leverages libraries like: OpenFermion, Qulacs, Jax, SciPy and many more

Basic Building Block: Expectation Values

this is a (parametrized) expectation value

$ E(\theta) = \langle \psi(\theta) \vert H \vert \psi(\theta) \rangle_{U(\theta)} = \langle H \rangle_{U(\theta)} $

of operator $H$
with respect to (parametrized) qubit wavefunction $\psi(\theta)$
prepared by circuit $U(\theta)$.

Tequila allows you to use expectation values as abstract functions.

Here is a simple example

U = tq.gates.Ry(angle="a", target=0)
H = tq.paulis.X(0)
E = tq.ExpectatioValue(H=H, U=U)

Basic Building Block: Expectation Values

The abstract expectation value can be compiled

f = tq.compile(E)

and afterwards used like a function (passing variable values as dictionary)

g = f({"a":1.0})

in this example we have:

  • the abstract expectation value E
  • the compiled expectation value f
  • the evaluated expectation value g (this is just a number)

Basic Building Block: Expectation Values

Compilation can be onto several backends that are either simulators or interfaces to quantum computers

f1 = tq.compile(E, backend="qulacs")
f2 = tq.compile(E, backend="cirq")
f3 = tq.compile(E, backend="qiskit")

exact = f1({"a":1.0})
simulated_samples = f1({"a":1.0}, samples=1000)
real_samples = f3({"a":1.0}, samples=1000, device="imbq_rome")

Combine Expectation Values:

Astract expectation values can now be combined to more complicated objects, like for example

F = 2.0*E
G = F**2 + tq.grad(F, "a")

again, resulting objects can be compiled and used like functions

g = tq.compile(F)
evaluated = g({"a":1.0})

Combine Expectation Values:

Here is a specific example:

$ f = e^{-\left(\frac{\partial E}{\partial a} + b\right)^2} $

F = ( tq.grad(E,"a") + tq.Variable("b") ).apply(numpy.exp)**2 
f = tq.compile(F)
  • with tq.grad(E,"a") we create the gradient (using the shift rule in the back)
  • with tq.Variable("b") we create a variable that can be used in the function
  • with A.apply(B) we create B(A) where B is a scalar function and A is a tequila object

Now lets create the gradient of this function: $\frac{\partial f}{\partial b}$

dF = tq.grad(F, "b")
df = tq.compile(dF)

see tequila tutorials and slides for explicit examples

Example from the tile slide:

source code

More complex gate parameters

standard parametrized $R_y$ gate

U = tq.gates.Ry(angle="a", target=0)

parametrized with the square of a variable

a = tq.Variable("a")
U = tq.gates.Ry(angle=a**2, target=0)

parametrized with the result of a compiled tequila function (consisting of combinations of expectation values)

U = tq.gates.Ry(angle=f, target=0)

not parametrized

U = tq.gates.Ry(angle=1.0, target=0)

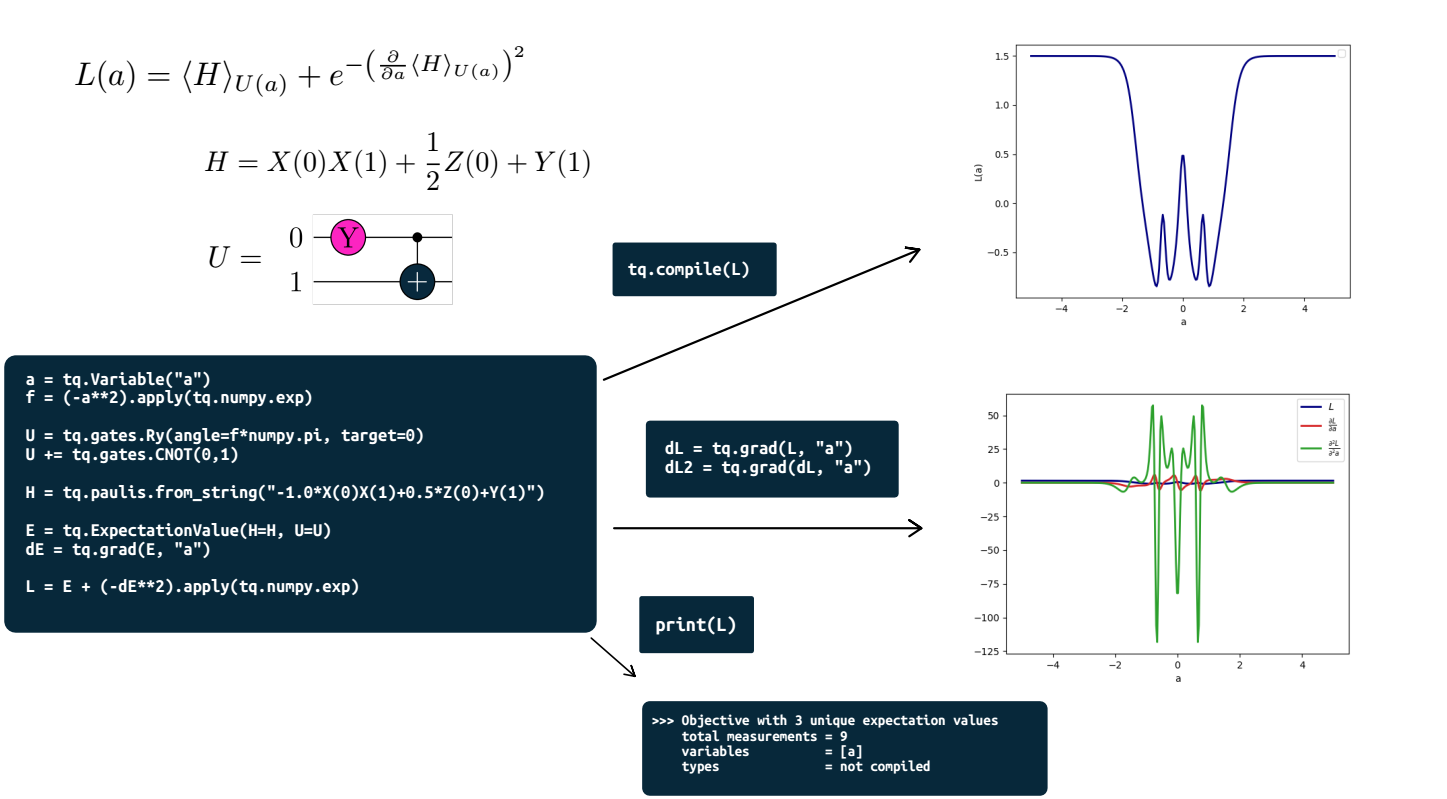
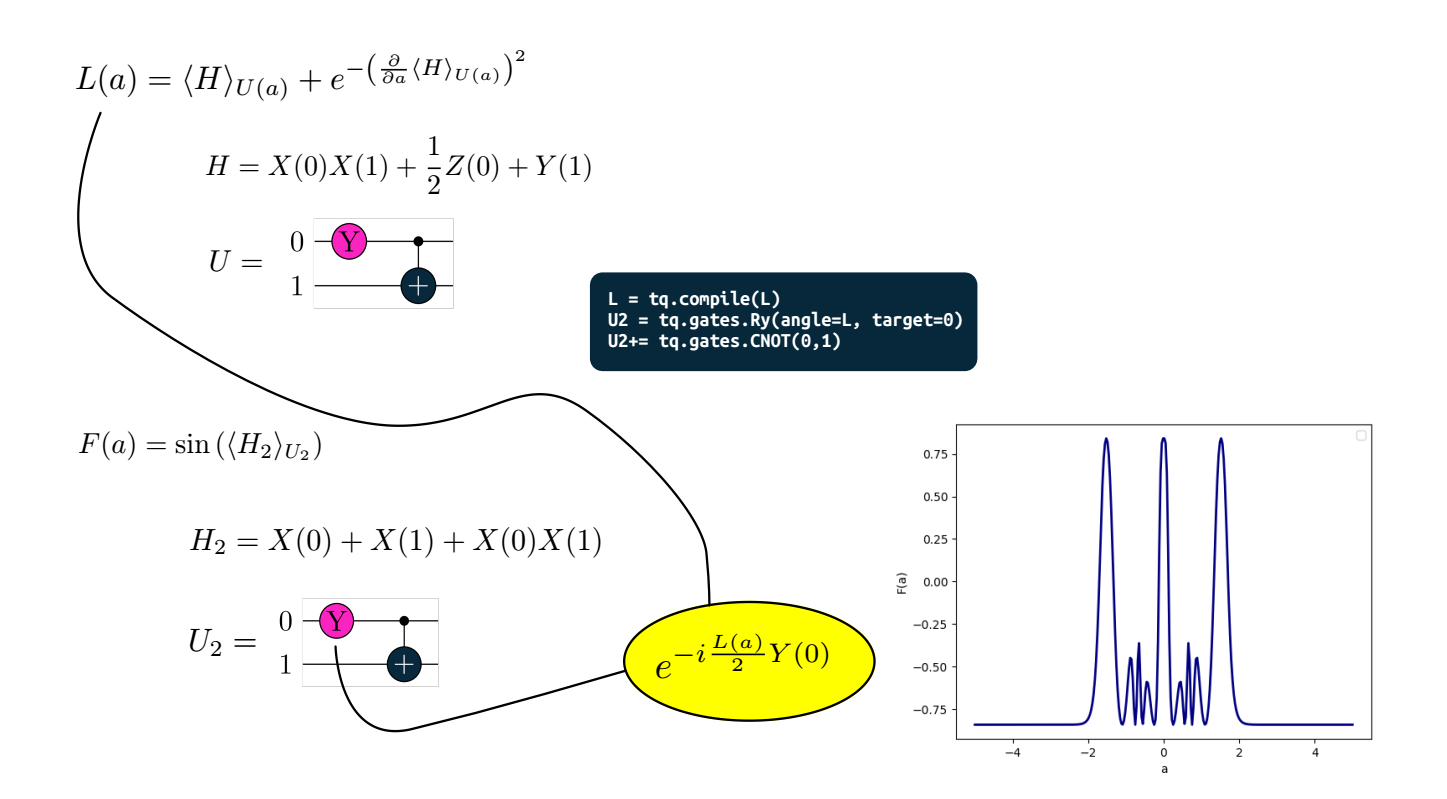
Nested example: Quantum function $L$ defines gate parameter of other quantum function $F$

source code

Some convenient quantum gates

Standard gates in tq.gates: H, X, Y, Z, Rx, Ry, Rz, S, CNOT, SWAP

Form controlled gates with control keyword

CRy = tq.gates.Ry(angle="a", target=0, control=1)
CCRy = tq.gates.Ry(angle="a", target=0, control=[1,2])

Multi-Pauli Rotations: $e^{-i\frac{a}{2} P}$

U = tq.gates.ExpPauli(paulistring="X(0)Y(1)", angle="a", control=None)

Qubit-Excitations: $e^{-i\frac{a}{2} G}$ with e.g. $G = -i(\sigma_i^- \sigma_j^+ - \sigma_i^+ \sigma_j^-) $

U = tq.QubitExcitation(target=[i,j], angle="a", control=None)
U = tq.QubitExcitation(target=[i,j,k,l], angle="a", control=None) 
U = tq.QubitExcitation(target=[i,j,k,l,m,n], angle="a", control=...)

Smart Compiler

U = tq.QubitExcitation(target=[0,2], angle="a", control=None)
...
E = tq.ExpectationValue(H=H, U=U)
f = tq.compile(E, backend=...)

if backend supports MultiPauli: 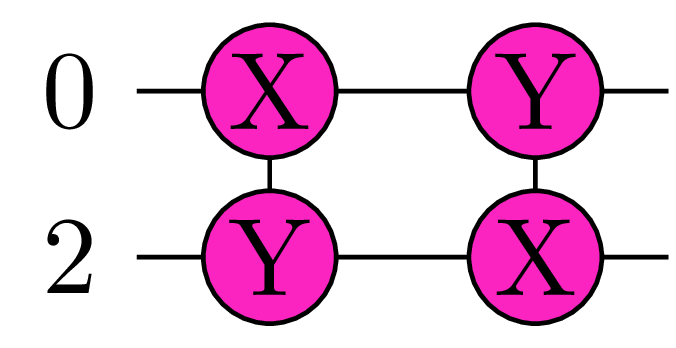if backend supports CRy: 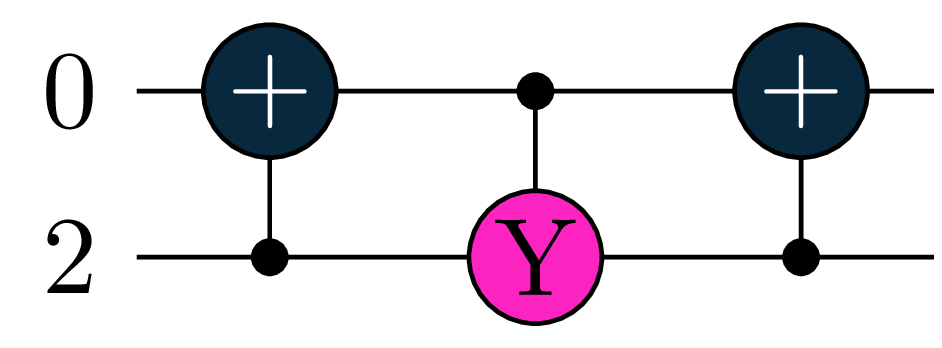otherwise:

Measurement Optimization

# full simulation is faster wihtout measurement optimization
E = tq.ExpectationValue(H=H, U=U)
# sampled runs are faster with measurement optimization
E = tq.ExpectationValue(H=H, U=U, optimize_measurements=True)

See papers by Izmaylov group (T.C. Yen, V. Verteletskyi, Z.P. Bansingh)
and the tequila tutorial

Optimizers

As tequila functions are just scalar functions, they can be minimized

result = tq.minimize(E)
final_value = result.energy
optimized_variables = result.variables
f = tq.compile(E)
final_value = f(optimized_variables)

useful

tq.show_available_optimizers()

see github tutorials on optimizers for more

Vectors, Matrices, Tensors

tq.QTensor class: Same as numpy.ndarray with abstract tequila functions

M = tq.QTensor(shape=[2,2])

M[0,0] = tq.Variable("a")**2
M[1,0] = tq.ExpectationValue(H=H, U=U)**2
M[0,1] = f**2
M[1,1] = 1.0

N = M.dot(M)

n = tq.compile(N)

evaluated_matrix = n({"a":1.0, "b":2.0, ...})

see github tutorials on QTensor for more
implemented as a qosf project (Gaurav Saxena)

QTensor: Example

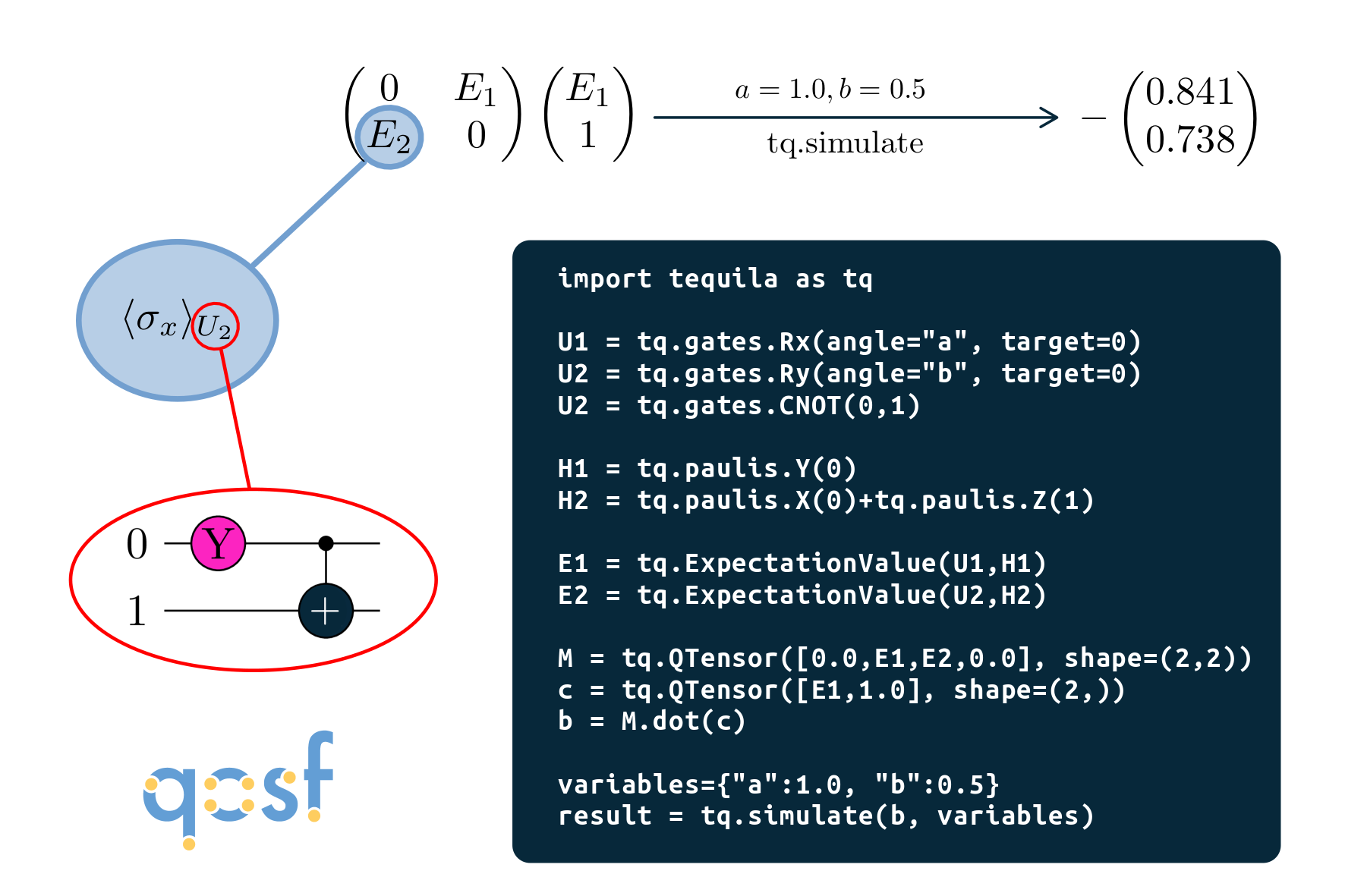
More:

Installation:

Linux and MacOS

pip install tequila-basic

recommended to install qulacs (fastest backend)

pip install qulacs

On Windows

pip install git+https://github.com/tequilahub/tequila.git@windows

Note: Windows version is less flexible (e.g. E**2 needs to be E.apply(numpy.square) here)

See github readme for more information